|
|
1.IntroductionActive control enables large telescopes by maintaining optical performance in the presence of perturbations. Active control algorithms have been optimized for large ground telescopes and are commonly used to compensate for manufacturing errors, gravitational and thermal distortions, and low-frequency errors induced by wind.1–5 By comparison, active control algorithms for space telescopes are less mature. The baseline control scheme for the first large active optical/infrared space telescope, the James Webb Space Telescope (JWST), is conceptually simple, consisting of measuring the wavefront error (WFE) every 2 days and using these measurements to apply corrections every 2 weeks as needed.6 This scheme satisfies the observatory’s requirements; however, alternative control algorithms may further improve the performance, providing lower and/or more stable WFEs and enhancing science capabilities. The difference in maturity between the control algorithms for active space telescopes such as JWST and active ground telescopes is due in part to differences in the wavefront control problems, which stem from differences in the observatory design constraints and environment. For an active space telescope, the control problem involves a trade between minimizing the WFE deviations and minimizing the number of corrections. Limited by the mass and volume constraints of a launch vehicle, active space telescopes generally use the science instruments to monitor the wavefront periodically.7–10 As a result, there is a significant cost associated with each wavefront measurement; since science observations and wavefront measurements cannot be performed simultaneously, each wavefront measurement reduces the observatory efficiency. This cost is amplified for control schemes that require a postcorrection wavefront measurement to verify the actuator motions, and it provides one incentive to limit the number of corrections. Additional incentives to avoid unnecessary control include the inability to repair or replace actuators that have exceeded their design lifetimes and, for cryogenic mirrors, the possibility of introducing heat with each actuator move. In the specific case of JWST, the mirror actuators are unpowered the vast majority of the time in order to meet overall thermal requirements for the telescope. In addition, high-speed continuous control is less necessary for an active space telescope at L2 since the dominant wavefront perturbations are driven by changes in the thermal environment, with timescales on the order of hours to days. These changes are caused by variations in the solar heating as the telescope attitude changes from one observation to the next. Minimizing degradations from such medium-timescale perturbations is the key challenge for active wavefront maintenance in space. Slower perturbations, such as those due to gradual degradation of a sunshield or insulation or to annual orbital variations in the distance to the sun, are readily corrected by a control scheme that operates on a timescale of days to weeks, and faster dynamical perturbations leading to pointing jitter can be partially controlled by an active fine steering mirror2 up to some control-bandwidth-limited frequency. The control problem for an active space telescope thus consists of weighing control costs against the benefits of correcting WFE perturbations that are a predictable byproduct of the observing schedule, which we determine and know in advance. This is a very different situation than the one faced by active ground telescopes, where the rapid weather-dominated disturbances require continual control, wavefront measurements and science observations are performed concurrently using separate dedicated hardware, and worn-out actuators can be replaced. In this paper, we investigate several methods for improving the control algorithms for active space telescopes at L2. We do not discuss the details of how the wavefront measurements are to be obtained nor how the desired controls are applied via spacecraft actuators; these topics have been discussed at length in other papers.6,7,11 Our focus here is on the question of how often sensing and control should take place and how multiple sensing measurements may be combined in order to optimize performance. Although our analysis is based on JWST specifically, the general approach taken is also applicable to other missions, such as the proposed Astrophysics Focused Telescope Assets (AFTA) and Advanced Technology Large-Aperture Space Telescope (ATLAST) mission concepts.12,13 Several of JWST’s driving science cases are exquisitely sensitive to variations in point spread function properties, for instance weak lensing studies of the early universe or coronagraphic observations of nearby exoplanets, and would benefit greatly from as stable a telescope as possible. Intrinsic wavefront sensor noise and calibration systematics likely set a fundamental limit of a few nanometers RMS. How closely can we approach that limit? The overall optical performance of JWST depends on contributions from many other factors besides the thermal perturbations we model here, including the telescope’s static WFE, the science instruments’ internal WFE, and uncontrolled high-temporal-frequency dynamical perturbations induced by the reaction wheels, Mid-Infrared Instrument (MIRI) cryocooler, and fuel slosh. Integrated modeling predicts a total telescope WFE in the range of 90 to 110 nm RMS,14 so the time-variable component (expected to be of order 60 nm) corresponds to a significant part of JWST’s overall optical error budget. Although fluctuations from transient dynamics occurring over timescales of hours can be comparable to thermal changes occurring over several days, the wavefront control architecture adopted for JWST supports wavefront control over relatively longer timescales and does not attempt to compensate for the transient perturbations. Rather, those are to be minimized through careful design of the observatory, avoidance of reaction wheel resonant frequencies, and tuning of the cryocooler settings. Our focus in this work is to consider the relative merits of different approaches for wavefront control at a cadence of days to weeks, so we acknowledge the importance of the dynamical terms in setting the fundamental performance limits but do not consider them further in this paper. Since the dominant WFE perturbations over longer timescales are due to thermal fluctuations, we have developed a combined thermal and wavefront model that tracks the temperature evolution over a sample mission and calculates the corresponding WFE (Sec. 2). A similar approach has been used successfully to track focus variations in the Hubble Space Telescope.15 Using this model, we first show that the WFE can be controlled passively by introducing scheduling constraints that limit the allowable sun angles for an upcoming observation based on the mean telescope temperature (Sec. 3). We then turn to strategies for active control: we describe the design and implementation of a predictive hybrid controller (Sec. 4.2) and assess its performance relative to simpler control strategies under a variety of assumed conditions (Sec. 4.3). This algorithm is designed to prevent the WFE from ever exceeding a desired limit instead of simply reacting after the limit has been exceeded; it uses an internal thermal model to predict when the WFE will exceed the threshold and schedules corrections in advance. As a result, the corrections are placed at more effective times, and the algorithm achieves a lower WFE without requiring significantly more corrections. We close (Sec. 5) with a summary of results and a look ahead to future work and the feasibility of implementation for JWST. 2.Thermal and Wavefront ModelDuring the course of a mission, an active space telescope such as JWST is rarely, if ever, in thermal equilibrium. The equilibrium thermal state is affected by the amount of solar heating, which depends on the attitude of the telescope relative to the sun. As a result, the equilibrium state is different for each observation, changing as the telescope slews from one science target to the next. Since a typical observation lasts a few hours, there is insufficient time for a cryogenic shielded telescope to equilibrate before the next slew; the thermal time constant for typical designs is on the order of days.16–18 As a result, the thermal state of the telescope is not a simple function of attitude, but rather a complex function of attitude history. As the thermal state changes during a mission, the thermally induced deformations in the observatory structures also vary, causing perturbations in the WFE (Fig. 1). Fig. 1Sample temperature and wavefront evolution for a repeated slew between two attitudes. Since an active space telescope is rarely in thermal equilibrium, the mean telescope temperature is not a simple function of attitude. During an observation, the temperature follows an exponential determined by the temperature at the start of the observation, the observation duration, and the equilibrium temperature associated with the sun angle. These parameters change with each observation, altering the temperature trajectory. The change in the wavefront error (WFE) with respect to some nominal state is determined from the temperature using a linear model. As an example, the temperature and RMS WFE evolution are shown for a square wave pointing schedule. 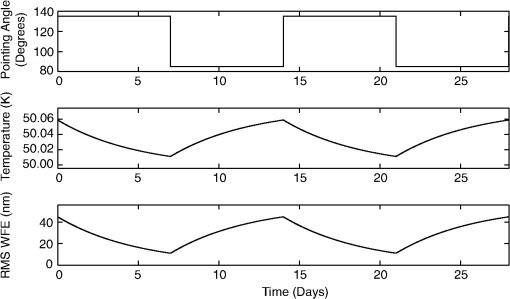 To investigate how the WFE evolves in response to changes in the thermal state, we have developed a combined temperature and wavefront model. This model assumes that all of the important dynamics can be determined to first order by tracking a single temperature that corresponds to the dominant deformation. As an example, distortions of the primary mirror backplane support structure are expected to dominate the WFE evolution for JWST, and these distortions correspond to changes in the average backplane temperature.17,19 The model also assumes that the thermal changes are caused only by variations in the spacecraft orientation with respect to the sun (hereafter “sun angle”). Although changes due to roll or other sources could be included in a more sophisticated model, these perturbations are small by comparison. As an example, JWST has an allowed pointing range of 85 to 135 deg between the telescope optical axis and the sun, set by the geometry needed to keep the telescope in the shade at all times (Fig. 2). Rotations azimuthally around the optical axis are relatively minor since they are restricted to a range of approximately to , and rotations around the JWST-to-sun axis, though unconstrained, do not affect the amount of solar heating.20 Fig. 2Attitude range. For the simulations, we assume that the spacecraft attitude range is identical to that of JWST20 (a). The hottest attitude corresponds to a sun angle of 85 deg (b), and the coldest attitude corresponds to a sun angle of 135 deg (c). Since thermal changes are predominately due to changes in the sun angle , we concentrate here on the effects of alone. 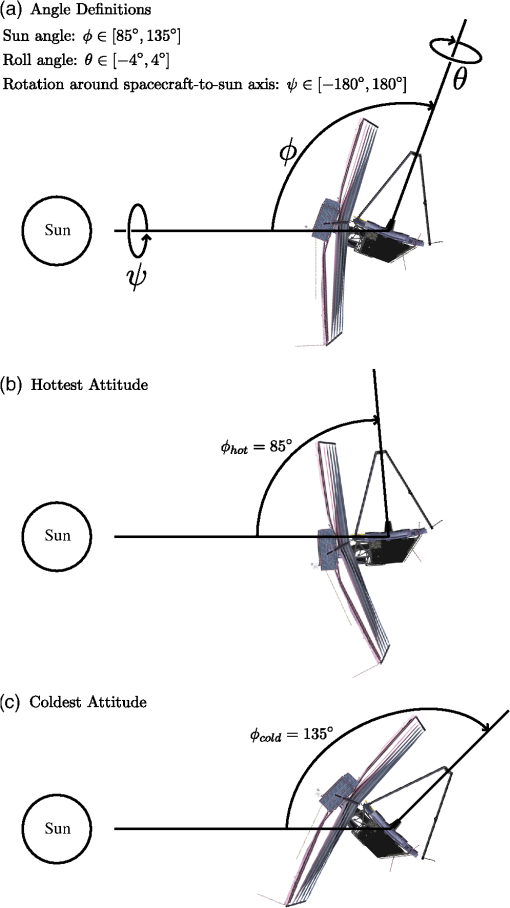 Since the equilibrium thermal state can change with each observation, the combined temperature and wavefront model follows three basic steps for each observation: determining the equilibrium temperature, calculating the temperature evolution, and relating the temperature to a WFE. In the equilibrium temperature model, each sun angle is associated with the equilibrium temperature the telescope would attain if left at that attitude for infinitely long. This temperature can depend, for example, on the projected area of the sunshield normal to the sun, which varies cosinusoidally with the sun angle. More generally, this relationship can be parameterized to second order as where the constants , , and are determined by fits to available thermal models or on-orbit measurements. (It is important to note that we are not advocating approximating cosinusoidal behavior using a quadratic model. The cosinusoidal variation is presented as a conceptual example of how the temperature might depend on the sun angle, but we have selected a more general quadratic model since there are likely additional effects that influence the specific temperature dependency.) In the case of JWST, detailed finite element modeling19 has concentrated on the hottest and coldest attitudes, so we fit , , and by considering these extreme cases. These attitudes determine the temperature range, and they are affected by the sunshield geometry and the pointing restrictions.During an observation, the mean telescope temperature is assumed to follow an exponential of the form where is the temperature at the beginning of the observation, is the time the observation begins, and is the thermal decay constant. While different portions of the observatory and spacecraft structure can have distinct time constants, finite element modeling results21 suggest that the simplifying assumption of a single time constant provides a reasonable first-order approximation of the more complex underlying physics. In general, the temperature at the start of observation , , will depend on the temperature at the end of observation , , and the slew duration. For the initial investigations in Sec. 4, we consider the worst-case thermal changes by neglecting slews and assuming that .After the temperature has been determined, the corresponding WFE is calculated using a linear model. For these calculations, it is convenient to consider the change in the WFE with respect to some nominal state, such as the long-term average optical state or the observatory’s best-achieved starting alignment. We denote this by : Since the temperature is bounded by and , it is particularly convenient to calculate changes in the WFE relative to the WFE at one of these limiting temperatures; we use . For simplicity, the wavefront model assumes that each coefficient in the expansion of the wavefront scales linearly with temperature; in the absence of control, the relative WFE is where the are the first Zernike coefficients specifying the change in WFE at the hottest temperature. As an example, the temperature and WFE trajectories for a hypothetical back-and-forth slew pattern between two attitudes are shown in Fig. 1.For the simulations that follow, we consider an active space telescope at L2 with thermal properties based on the requirements for JWST. The allowable sun angles are identical to those for JWST,20 ranging from 85 to 135 deg. The hottest attitude is 85 deg and the coldest is 135 deg, as shown in Fig. 2. The thermal decay constant is assumed to be , based on the JWST requirement that the WFE is sufficiently stable to achieve RMS over a 2-week period in the absence of wavefront control,17 and the Zernike coefficients are similarly chosen such that the RMS WFE changes by approximately 56 nm for the worst-case slew. These coefficients, along with the remaining thermal model parameters such as the temperature range, are loosely derived from the results of detailed finite-element thermal modeling of the temperature evolution following a worst-case cold-to-hot slew.19,21 3.Limiting the WFE Using Schedule RestrictionsSince the WFE perturbations are driven by changes in the sun angle, they are a byproduct of the observing schedule, which we know and determine in advance. As a result, we can control the WFE evolution passively by introducing scheduling constraints as part of the schedule generation process. This type of approach has been studied for managing the spacecraft momentum,22 which also depends on the sun angle, and the same or similar constraint mechanisms in the scheduling software could be extended to consider the WFE. These constraints can in principle either limit the WFE change during an observation or ensure that the total WFE change never exceeds a specified limit. For the thermal model we consider, both approaches are suitable for typical observations, allowing most if not all of the sky. However, in practice limiting the total WFE change may be too restrictive since the constraints limit the field of regard for long observations. Since changes in the WFE are directly related to changes in the telescope temperature, the scheduling constraints are derived from temperature restrictions; the basic principle is to generate schedules that do not cause the telescope temperature to experience extreme swings or deviate from a specified range. Limiting the WFE change during an observation, for example, corresponds to defining a range of allowable final temperatures based on the initial temperature and the observation duration. Similarly, ensuring that the total WFE change remains below a specified threshold corresponds to requiring that the temperature remain at all times within a range determined by the reference temperature (for which there is no WFE). In each case, the temperature limits determine the maximum and minimum equilibrium temperatures, which correspond to the minimum and maximum allowable sun angles, respectively, for the next spacecraft attitude in the schedule. As a result, the scheduling constraints are derived by relating the desired WFE condition to restrictions on the final temperature, determining the limiting equilibrium temperatures, and calculating the corresponding sun angles. As an example, to ensure that the WFE change during an observation does not exceed a desired threshold , we require that where and are the times at which the observation begins and ends, respectively. Using Eq. (4), we can rewrite this condition as where is the temperature at the end of the observation. Solving for , we find that Eq. (5) is satisfied if where and For an observation of duration , these limiting values for correspond to equilibrium temperatures of and respectively, where the additional restrictions ensure that the temperature remains within the range . Substituting these equilibrium temperatures into Eq. (1), we find that the maximum and minimum sun angles are As a result, Eq. (5) is satisfied if . For instance, suppose we wish to keep the WFE change below 10 nm for observations up to 2 days in length. Then, for , observations are allowed at sun angles between 85 and 131 deg, using our thermal model. In general, the allowed sun angles vary depending on the initial temperature and observation duration, as shown in Fig. 3.Fig. 3Restricting the WFE change during an observation. Since the WFE perturbations are driven by changes in the sun angle , we can control the WFE passively by introducing scheduling constraints. To limit the WFE change during an observation, we require that , where and depend on the equilibrium angle associated with the temperature at the start of the observation, . These restrictions limit the size of slews from , with the excluded sun angles requiring larger slews. Since the angle boundaries approach as the observation duration increases, the entire field of regard remains accessible regardless of the observation duration, provided that is consistent with the restrictions. Conversely, for an arbitrary starting temperature , the entire field of regard can be observed if the observation duration is sufficiently brief. As an example, the plotted constraints ensure that the WFE changes by no more than 10 nm during an observation. 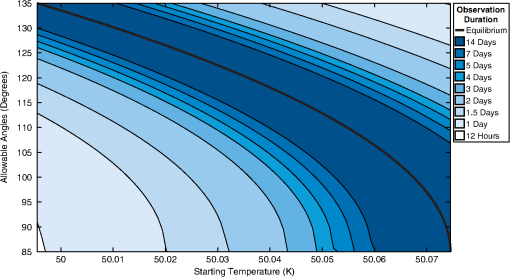 Similarly, to keep the RMS WFE below at all times, we require that the temperature remain within the bounds that correspond to the maximum allowable WFE. Since we have selected as the reference temperature, we know that , so . In this case, we only need to find . Using Eq. (4), we can write the WFE requirement as Solving for , we find that the temperature requirement is where For an observation of duration , corresponds to an equilibrium temperature of and a minimum sun angle ofAlthough short-duration observations are allowed under either set of angle restrictions using our thermal model and , the different approaches exclude different regions of the sky as the observation duration increases. For the first approach, restricting the WFE change during an observation, the range of allowable sun angles depends on the equilibrium sun angle associated with the initial temperature, with excluded sun angles corresponding to large slews from as shown in Fig. 3. (The actual slew size required to reach one of the allowable sun angles may vary: the sun angle during the previous observation is not necessarily near since the telescope is rarely in thermal equilibrium.) As the observation duration increases, the difference between the initial and limiting temperatures must decrease in order to satisfy the temperature requirement, so the angle boundaries approach . As a result, any part of the sky remains accessible regardless of the observation duration, provided that the initial temperature is consistent with the restrictions. These angle restrictions also allow more of the sky at hotter attitudes due to the quadratic model for [Eq. (1)]; since changes less rapidly near the hottest attitude, larger slews from can be tolerated. By comparison, the second restriction approach preferentially excludes attitudes that are further from the reference attitude. Although the entire sky is accessible for typical short observations in our example, the scheduling constraints restrict the field of regard as the observation duration increases, which can decrease the scheduling efficiency and potentially preclude some observations. As a result, it may be more practical to use the restrictions derived from limiting the WFE change during an observation. Although incorporating sun angle restrictions in the observing schedule is a promising technique for passively controlling the WFE, in practice this method would be complicated to implement given the many other constraints that must be considered as part of scheduling.23 Detailed simulations of mission scheduling are beyond the scope of this paper, but any potential implementation of this method would need to carefully assess the efficiency impacts from the additional constraints. 4.Limiting the WFE Using Optical ControlAlthough the active control algorithms for ground telescopes are typically variations on classical control laws,4,24–27 the control problem for an active space telescope is more naturally expressed as a hybrid control problem. Hybrid systems consist of both continuous and discrete subsystems that interact, and they come in many forms.28–33 As an example, the interaction between the temperature in a room and a thermostat constitutes a hybrid system: the continuous temperature dynamics are affected by the discrete dynamics of the thermostat, which turns on and off depending on the temperature.28 Other hybrid control applications include manufacturing processes,34 aircraft collision avoidance,35 automated highway systems,36 automotive engine control,37 life support systems for manned space exploration,38 and allocating water based on seasonal snowmelt cycles.39 In the case of an active space telescope, the continuous WFE evolution is affected by both discrete and continuous dynamics even in the absence of optical control. In the uncontrolled case, the WFE is directly proportional to the temperature [Eq. (4)], and the continuous temperature dynamics are affected by the start of a new observation; changes in the sun angle alter the exponential. When optical control is added, the WFE is the sum of the temperature-induced error and the control vector : This control vector is updated at discrete times rather than continuously, with the corrections determined by the specific control algorithm:Although the wavefront control process could be fully automated in theory, we will consider the case where ground intervention is required because this adds the complication of time delays and is the case for JWST.40 In this scenario, wavefront measurements are sent from the spacecraft to a ground station for analysis, after which a new set of commands, including any wavefront corrections, is sent to the spacecraft. Two time delays account for the total amount of time that elapses during this process (Fig. 4). The first delay, , accounts for the time required for wavefront measurements to be sent from the spacecraft and processed on the ground. The second delay, , accounts for the time required for a set of commands to be sent to the spacecraft. It is assumed that no new measurements are taken until after both delays have passed. Fig. 4Time delay definitions. In the wavefront control process, new measurements are sent to the ground for analysis, after which updated commands, including revised wavefront corrections, are sent to the spacecraft. Two time delays account for the total amount of time that elapses during this process: accounts for the time required for wavefront measurements to be sent to the ground and processed, and accounts for the time required for a set of commands to be sent to the spacecraft.  In addition to time delays, the wavefront control process can also be complicated by the presence of noise. Due to the hybrid nature of the control problem and the relative infrequency of the wavefront measurements, this noise is not readily handled by applying classical approaches such as a Kalman filter; this is a case where the model itself changes faster than the measurements are taken. At the start of each observation, the change in sun angle alters the equilibrium temperature, which in turn alters the temperature and wavefront trajectories. Since wavefront measurements are taken every few days, while typical observations last a few hours, the wavefront trajectory can switch many times between measurements. As a result, it is not trivial to estimate the true wavefront evolution using a sequence of noisy measurements. To investigate the optical performance that can be achieved with infrequent wavefront control, we have evaluated three control algorithms according to two competing metrics: the number of actuator moves and the amount of time spent over the correction threshold. Two of these algorithms are variations on the baseline control scheme for JWST, and the third is our predictive controller that uses an internal temperature and wavefront model to determine in advance when corrections will be needed (Sec. 4.2). Using multiple observing schedules (Sec. 4.1), we compare these algorithms under a variety of assumed conditions, including cases with noise and model error (Sec. 4.3). These comparisons show that while all three algorithms successfully maintain the wavefront even with substantial measurement noise, the predictive controller generally provides the best performance. 4.1.Mission SchedulesTo assess the strengths and weaknesses of wavefront control algorithms, it is useful to consider two types of schedules: simple schedules that are easily understood and more realistic schedules that approximate the types of observations expected on orbit. In the simulations that follow, we will use square wave schedules as well as schedules based on the Science Operations Design Reference Mission (SODRM) 2012 schedules for JWST.23 The square wave schedules represent repeated worst-case slews, with the observatory oscillating between the hottest and coldest attitudes with a period of 1 to 56 days [Fig. 5(a)]. Since we assume that the attitude changes occur instantaneously, these schedules consider the worst-case thermal changes for each period. In contrast, the SODRM-based schedules simulate more realistic hypothetical mission scenarios based on a detailed population of candidate observations. We consider 15 realizations of the sample mission schedules, which represent different orderings of the same underlying pool of observations; an example is shown in Fig. 5(b). Fig. 5Mission schedules. To evaluate the performance of the wavefront control algorithms, we consider two types of schedules: square wave schedules that represent repeated worst-case slews between the hottest and coldest attitudes (a), and hypothetical mission schedules based on the SODRM schedules for JWST23 (b). Fifteen such SODRM schedules were provided to us by the JWST planning and scheduling system developers. 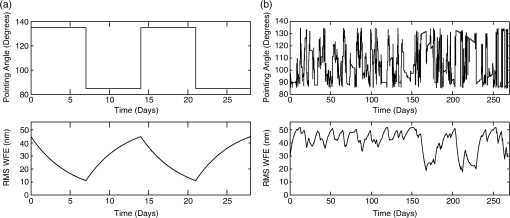 4.2.Control SchemesFor an active space telescope, the WFE evolution depends on the control scheme in addition to schedule parameters such as the sun angle changes and the observation durations. Control schemes that use a sequence of wavefront measurements to correct excursions at regular intervals, for example, perform differently than schemes that preemptively correct the wavefront before the error exceeds a desired limit. To investigate the effectiveness of each approach, we have developed three control algorithms: baseline and averaging algorithms that correct every 2 weeks as needed, and a predictive algorithm that uses an internal model to determine in advance when corrections will be needed. 4.2.1.Baseline and averaging algorithmsFor the baseline and averaging algorithms, we use a control scheme that is similar to the baseline scheme for JWST.6 The WFE is measured every 2 days, and the measurements taken during the last 2-week period are used to determine if a correction is needed. For the baseline algorithm, only the most recent measurement is used. At the end of each control period, the RMS WFE from is compared against the correction threshold , and if the error exceeds , a correction is sent to the spacecraft [Fig. 6(a)]. This correction consists of the additive inverse of : This algorithm is analogous to the classical feedback control laws that are typically used to actively control large ground telescopes;24–27 it is similar to a proportional controller with a logic-driven gain operating on a 2-week timescale rather than continuously. It may seem inefficient or overly simplistic to simply discard six out of seven measurements. However, given the time-variable wavefront evolution as noted above, it is not straightforward to combine measurements from different times, and how to do so for JWST has not yet been specified. This scenario intentionally represents a simplest possible algorithm against which we can compare more sophisticated approaches.Fig. 6The wavefront control algorithms. To investigate the effectiveness of various wavefront control approaches, we have developed three control algorithms: baseline (a) and averaging (b) algorithms that are variations on the baseline control scheme for JWST,6 and a predictive control algorithm (c) that uses an internal thermal model and knowledge of the observing schedule. 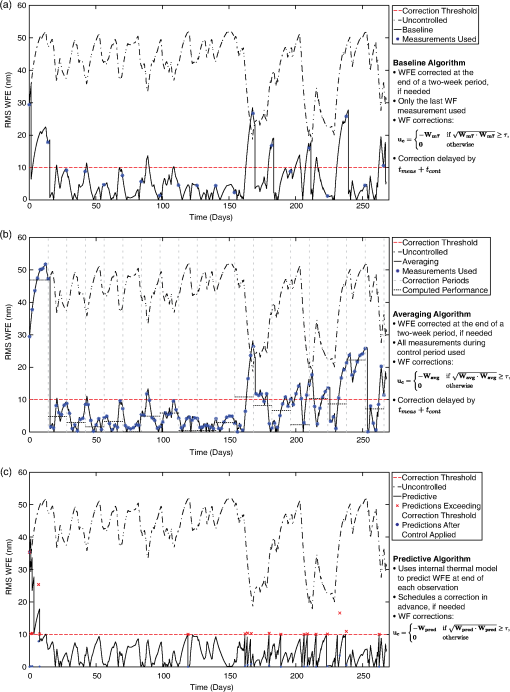 The averaging algorithm, on the other hand, uses all of the wavefront measurements taken during the last control period. These measurements are used to construct a vector of the average wavefront coefficients during the last 2 weeks, , and a correction is issued if the corresponding RMS WFE exceeds [Fig. 6(b)]. This correction consists of the additive inverse of : Since the baseline and averaging algorithms use a sequence of measurements to determine if a correction is required, there is an implicit assumption that the WFE during the previous correction period is representative of the WFE during the upcoming period. As a result, these algorithms are expected to perform best in situations where the WFE variation is low relative to . It is also worth noting that these algorithms issue corrections only after the RMS WFE has exceeded , and these corrections are delayed by . 4.2.2.Predictive algorithmSince the wavefront perturbations are a byproduct of the observing schedule, it is possible to predict when the WFE will exceed the correction threshold and to schedule an appropriate correction in advance. Due to the hybrid nature of the system model, we have developed a hybrid predictive controller rather than using a classical predictive control algorithm.41 Our algorithm uses knowledge of the observing schedule and an internal thermal model to predict the WFE at the end of each observation, and it schedules a correction whenever the prediction exceeds the threshold. The algorithm also has the option of updating its internal model as wavefront and/or temperature measurements are taken in order to improve the accuracy of its predictions. In practice, the predictive control algorithm would likely reside at a ground station, where it would be used to generate a set of predictions up through a preset time rather than in real time. For instance, predictions could be generated for the next 2 weeks as part of the preparation of short-term schedules. As new measurements became available, the algorithm would update its internal model and generate a set of revised predictions. Since any new instructions arrive at the spacecraft after a total delay of , it would be particularly convenient to generate a set of predictions from to , where and are the times at which the most recent measurement and the next scheduled measurement are taken, respectively [Fig. 6(c)]. For simulations, the repeated calculations associated with model updates are unnecessarily inefficient, and it is advantageous to structure the predictive control algorithm differently. Due to the time delays, a measurement can be available for use on the ground, on the spacecraft, or neither. As a result, there are three possible information availability states if only one measurement type is used for model updates, and nine possible states if both temperature and wavefront measurements are used, For control purposes, only the information available to the spacecraft matters—while new predictions can be generated on the ground as soon as a measurement is received, this updated model cannot be used to alter the wavefront for observations occurring between times and . To track the flow of information throughout the system, our implementation of the predictive controller contains nine submodels, each containing the information available to the ground station and the spacecraft for one of the information states. A logic framework tracks the information state of the system and identifies the appropriate submodel to use; this framework also updates the submodels appropriately as the various delays pass. We emphasize that this approach is a computational convenience to speed simulations by considering all cases in parallel, not a required architecture.At the beginning of an observation, the predictive controller uses the information available to the spacecraft to predict the temperature and WFE at the end of the observation. The prediction model has the same basic structure as the physical model presented in Sec. 2, although it is more convenient to write the prediction for the thermally induced wavefront coefficients, , in slope-intercept form to allow for model updates: where and are the slopes and offsets, respectively, for the lines relating the temperature to the wavefront coefficients. It is important to note that the model parameters, such as the equilibrium temperatures and the thermal time constant, that are used in the predictive controller’s model will not in general be exactly equal to the true values representing the behavior of the spacecraft. We investigate in Sec. 4.3.5 cases of substantial error in the model parameters.If the WFE prediction exceeds the correction threshold , a correction is determined and applied. (In our simulation framework, there is no need to wait for a delay to pass since all delays have been incorporated in the model structure.) The wavefront correction can take several forms, including the additive inverse of the predicted wavefront coefficients at the start, end, or midpoint of the observation. We use the predicted wavefront coefficients at the time half of the WFE change during the observation has occurred, : To allow for independent temperature and wavefront model updates, our implementation of the predictive controller is structured such that the temperature model updates as temperature measurements become available, and and update as wavefront measurements become available. For a temperature update, is reset to match either the last measurement or the output of a state estimator. For a wavefront update, the last wavefront measurements and the corresponding temperature predictions are used to calculate the best-fit line for each wavefront coefficient; and are then reset to match the slopes and offsets for these lines. In this paper, we concentrate on using wavefront measurements only since that is the case relevant to JWST,40 although in general, temperature measurements could also be incorporated if the temperature sensors on the spacecraft and telescope were sufficiently precise. 4.3.Comparisons of Algorithm PerformanceThe performance of a wavefront control algorithm depends on the input schedule; control parameters, such as the sensing frequency and the correction threshold; and sources of error, including wavefront sensing noise and model error. To investigate the impact of each of these factors and assess the relative strengths of the control algorithms, we compare the performance of each algorithm under a variety of conditions, using a baseline correction threshold of 20 nm, which corresponds to approximately one third of the allowed wavefront variability in the absence of control for JWST.42 As we will show, each algorithm can control the wavefront successfully, with the predictive controller generally providing the best optical performance, even in the presence of substantial noise and model error. In the following sections, we first define the criteria used to assess the performance of each algorithm (Sec. 4.3.1). Then, we use highly simplified schedules to illustrate how the performance depends on the observation duration and the correction threshold (Sec. 4.3.2). Finally, we use more realistic schedules to investigate the effects of varying the mission schedule (Sec. 4.3.3), wavefront sensing noise (Sec. 4.3.4), and predictive model error (Sec. 4.3.5). 4.3.1.Performance metricsTo evaluate the optical performance, we consider two main metrics: the amount of time the RMS WFE exceeds the correction threshold and the total number of corrections commanded. When considered together, these metrics describe how successfully an algorithm achieves the competing goals of minimizing the RMS WFE and minimizing the number of wavefront corrections. We remind readers that corrections take nonzero time to apply (on the order of 100 min for JWST including mirror move time and postmove additional wavefront sensing for validation) and thus minimizing the number of corrections helps maximize the overall mission efficiency. (Note that while we consider both the RMS WFE and the number of corrections, we do not define a single metric that weights them together.) To neglect any transient effects associated with the simulation’s initial conditions and the first corrections, these metrics are calculated for the steady-state response, which is defined as starting on Day 35 for the SODRM-based schedules; by this time, the temperature dynamics are no longer affected by the initial conditions, and the algorithms have had at least two opportunities to issue corrections. For each simulation, we construct a time history of the RMS WFE, . [We remind readers that is the differential WFE measured with respect to the nominal alignment state as shown in Eq. (3), not the total WFE.] To gain additional insight into the wavefront response without plotting each time history, we calculate two quantities: the mean of all the RMS WFE data points in steady state, and the corresponding standard deviation. Taken together, these quantities describe the overall magnitude of the RMS WFE and the amount of variation during the simulation. 4.3.2.Effects of observation duration and correction thresholdIn the absence of noise, the observation duration and the correction threshold determine how aggressively an algorithm must correct in order to keep the RMS WFE below . Longer observations create larger wavefront changes, increasing the likelihood that the RMS WFE will exceed by the end of the observation, and lower thresholds allow less leeway for wavefront variations before a correction is needed. As a result, the number of corrections and the amount of time spent over the correction threshold both depend on the observation frequency and . To investigate how the performance is affected by the observation frequency, we consider square wave schedules with periods ranging from 1 to 56 days. In the absence of optical control, the RMS WFE for this type of schedule oscillates around the RMS WFE associated with the mean temperature [Figs. 5(a) and 7(a)]: where As the observation duration increases, there is more time for the wavefront to evolve, leading to larger changes; this behavior is reflected in the standard deviation, which increases with wave period [Fig. 7(b)]. For periods less than 14 days, the standard deviation is less than 10 nm, which is half the correction threshold. As a result, the RMS WFE passively remains below 100% of the time, and none of the control algorithms issue corrections in steady state [Figs. 7(c) and 7(d)].Fig. 7The effects of observation duration. In the absence of optical control, the RMS WFE for a square wave schedule oscillates around the RMS WFE associated with the mean temperature (a), with longer observation durations corresponding to larger WFE changes (b). For durations less than 2 weeks, the WFE variation is small enough that the RMS WFE remains below a correction threshold of 20 nm 100% of the time without optical control (d). As a result, none of the control algorithms issue corrections for these periods (c). [Note that the mean RMS WFE has been subtracted for the uncontrolled case in (d) since it is well known.] For periods longer than 2 weeks, the effectiveness of the baseline and averaging algorithms depends on the wave period, and it is possible to find cases where the algorithms lead to worse performance than the uncontrolled case. Of the three algorithms, the predictive controller performs the best, holding the RMS WFE below 100% of the time for each period without requiring significantly more corrections than the other algorithms. 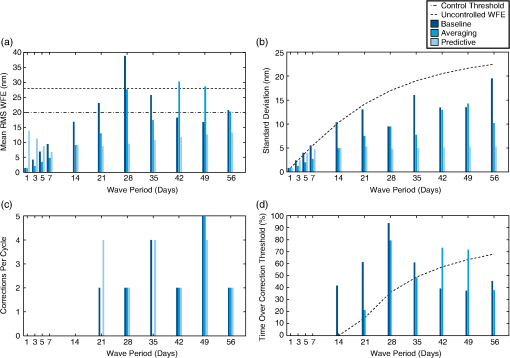 Since the baseline and averaging algorithms determine if a correction is needed at regular intervals, the optical performance for these algorithms depends on the relationship between the wave and control periods. The baseline algorithm is particularly sensitive to the timing since it uses only one measurement. When the wave and control periods are the same and in phase, for example, the baseline algorithm may issue no corrections even though the RMS WFE exceeds 41.6% of the time [Figs. 7(c) and 7(d)]. It is also possible to find cases where the optical performance is worse with these algorithms than without any control, although these pathological scenarios are not expected on orbit. As an example, for a square wave schedule with a 28-day period (twice the control period) and the same phase as the control cycle, the algorithms more than double the amount of time that the RMS WFE exceeds despite issuing corrections at every opportunity: the RMS WFE exceeds 79% of the time for the averaging algorithm and 94% of the time for the baseline algorithm, compared to 36% of the time if uncontrolled. Even when the baseline and averaging algorithms improve the optical performance relative to the uncontrolled case, the time spent over the correction threshold is limited to approximately 37% at best for the periods considered. By comparison, the predictive algorithm consistently improves the optical performance, holding the RMS WFE below 100% of the time without requiring significantly more corrections than the other algorithms. The predictive algorithm achieves this performance by placing the corrections at more effective times, scheduling them for points in the observing cycle where the RMS WFE changes rapidly and is about to exceed . For wave periods longer than 2 weeks, this scheduling actually leads to a lower mean RMS WFE than the averaging algorithm (Fig. 7). Similarly, during the course of a sample mission, the predictive algorithm provides the best optical performance, holding the RMS WFE below at least 99.8% of the time on average. If we reduce below approximately 15 nm, the number of corrections required to maintain this performance increases significantly, from an average of 6.7 corrections at 15 nm to 53 corrections at 5 nm (Fig. 8). As a result, the performance of the noiseless, error-free predictive algorithm is limited only by the number of corrections that are permissible. By comparison, the performance of the averaging and baseline algorithms is limited by the 2-week correction period; for thresholds less than 10 nm, these algorithms cannot correct aggressively enough to keep the RMS WFE below during periods where the wavefront changes rapidly, such as during long observations following large slews. Consequently, the time over the correction threshold increases as decreases, while the number of corrections does not change significantly for the baseline and averaging algorithms. Fig. 8Selecting a correction threshold. For the predictive controller, the choice of correction threshold for a sample mission is limited only by the number of corrections; this algorithm holds the RMS WFE below at least 99.8% of the time for thresholds as low as 5 nm but requires an increasing number of corrections for . For the baseline and averaging algorithms, the choice of correction threshold is limited by the correction period, which is fixed at 2 weeks; for , these algorithms cannot correct aggressively enough to keep the RMS WFE below at times when the wavefront changes rapidly. 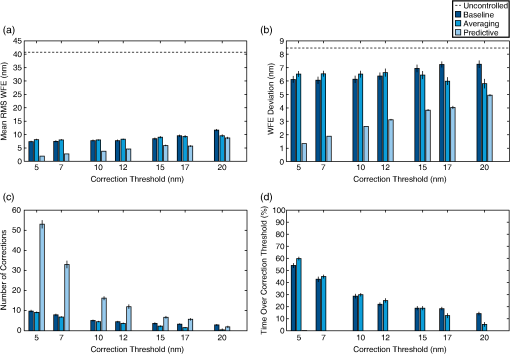 4.3.3.Effects of mission scheduleTo investigate how the optical performance varies with different mission schedules, we compare the results for the 15 SODRM-based sample mission scenarios. As shown in Table 1, for the predictive algorithm consistently holds the RMS WFE below 100% of the time, requiring 0 to 5 corrections depending on the schedule. This consistency is to be expected since the predictive algorithm is designed to correct the wavefront before the RMS WFE exceeds ; it may, however, require a different number of corrections to achieve this performance depending on the specific schedule. Table 1Baseline, averaging, and predictive algorithm performance for the sample mission scenarios.
The performance of the baseline and averaging algorithms, by comparison, can vary considerably with schedule since these algorithms rely on a sequence of measurements to determine when a correction is required. The wavefront measurements taken during a 2-week period are not always representative of the wavefront during the next 2-week period, and the WFE can at times temporarily exceed in between measurements without affecting the correction schedule. The baseline algorithm is particularly sensitive to the measurement timing since it uses only a single measurement, and it generally provides the worst performance. For the 15 schedules considered, the baseline and averaging algorithms hold the RMS WFE below 75.4% to 93.0% and 78.1% to 100% of the time, respectively (Table 1). Although the baseline and averaging algorithms are sensitive to the choice of mission schedule, it is not straightforward to predict whether a given schedule will prove challenging. As an example, for the schedules considered, the averaging algorithm in the best case holds the RMS WFE below 100% of the time without issuing any corrections in steady state. However, at least one of these “best” schedules contains larger wavefront changes than the schedule with the worst performance [Fig. 9(a)]. Similarly, the best schedule for the baseline algorithm contains larger wavefront changes than the worst schedule [Fig. 9(b)]. In general, it appears that the measurement timing is particularly important for the baseline and averaging algorithms. Adjusting this timing based on knowledge of the observing schedule may improve the performance, but the resulting algorithm would begin to resemble the predictive algorithm. To some extent, these behaviors just reflect the relatively simple definitions of the baseline and averaging algorithms, and point toward the need for a more nuanced approach like the predictive algorithm. Fig. 9Sensitivity to the mission schedule. Since the baseline and averaging algorithms use a sequence of wavefront measurements to determine when a correction is required, they are sensitive to the measurement timing, and their performance can vary considerably for different mission schedules. For the 15 schedules considered, the averaging and baseline algorithms hold the RMS WFE below 78.1% to 100% and 75.4% to 93.0% of the time, respectively. It is not straightforward to predict whether a given schedule will prove challenging. One of the best schedules for the averaging algorithm contains larger changes than the worst schedule (a), and the same is true for the baseline algorithm (b). 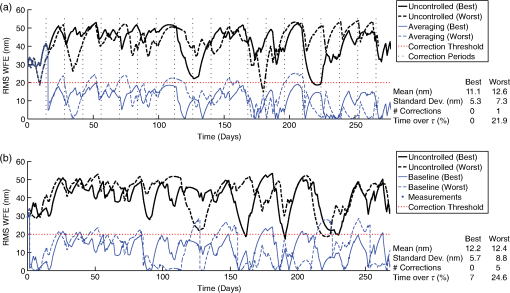 4.3.4.Effects of wavefront sensing noiseAlthough wavefront sensing noise can introduce errors in the correction process, the three control algorithms are not explicitly designed for noise rejection. To investigate whether these algorithms are sensitive to noise as a result, we add zero-mean Gaussian noise to each measurement taken during the sample mission scenarios. This noise is randomly distributed across all of the Zernike coefficients and has a standard deviation of 1, 5, or 10 nm. Twenty-five trials are conducted for each noise case and averaged together to obtain the final result. When the performance is averaged over all of the sample schedules, all of the algorithms successfully hold the RMS WFE below at least 80% of the time, even when the noise level is equal to half the correction threshold (Fig. 10). Of the three algorithms, the baseline algorithm typically provides the worst performance, holding the RMS WFE below 87% of the time at best, compared to 95% of the time for the averaging algorithm and 92% to 100% for the predictive algorithm. The averaging algorithm is least affected by the noise, spending approximately the same amount of time over the correction threshold and issuing the same number of corrections in each case. This behavior is to be expected since the mean RMS WFE during a correction period is relatively unaffected by zero-mean noise. The predictive algorithm, by comparison, generally provides the best optical performance, holding the RMS WFE below over 98% of the time even with measurement noise levels as high as 5 nm. Fig. 10Sensitivity to noise (averaged over all schedules). Although the three control algorithms are not explicitly designed for noise rejection, they all successfully hold the RMS WFE below at least 80% of the time on average, even when the noise level equals half the correction threshold. The averaging algorithm is the least sensitive to noise, performing comparably in each scenario, while the predictive algorithm generally provides the best optical performance. However, the predictive algorithm is sensitive to noise, requiring significantly more corrections as the noise level increases. For 10 nm noise, the relative performance of the predictive and averaging algorithms depends on the specific schedule. 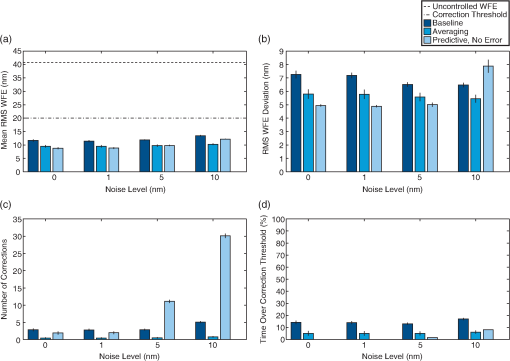 If the noise level is increased to 10 nm, the relative performance of the predictive and averaging algorithms depends on the specific mission scenario. The predictive algorithm achieves a lower time over the correction threshold for 33% of the scenarios we considered. As an example, for the schedule shown in Fig. 5(b), the predictive algorithm holds the RMS WFE below 100% of the time in the absence of noise, but drops to 91% as 10 nm noise is added (Fig. 11). In this case, the predictive controller even with noise performs much better than the averaging controller with zero noise, which achieves only 83% of the time under the threshold. Fig. 11Sensitivity to noise (sample schedule). Although the predictive algorithm is sensitive to noise, it can outperform the averaging algorithm even with substantial measurement noise. For the schedule shown in Fig. 5(b), the predictive algorithm with 10 nm noise holds the RMS WFE below 91% of the time, while the averaging algorithm achieves only about 85% at best. 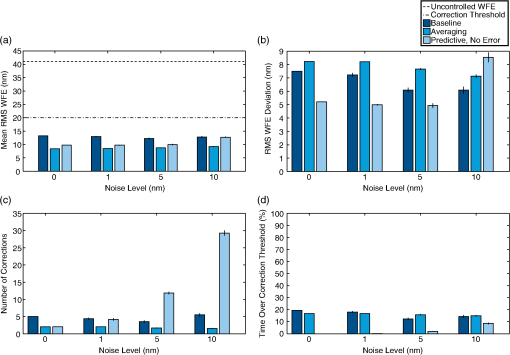 While the averaging algorithm is sensitive to schedule and insensitive to noise, the reverse is true for the predictive algorithm. As the noise level increases, the predictive controller works harder to maintain the wavefront, issuing significantly more corrections [Figs. 10(c) and 11(c)]. The aggressive correction schedule also leads to higher variation in the RMS WFE [Figs. 10(b) and 11(b)]. Our implementation of the predictive controller is sensitive to noise since it uses all of the last wavefront measurements to update its internal temperature-to-wavefront model; one particularly noisy measurement can affect the accuracy of subsequent WFE predictions (Sec. 4.2.2). More sophisticated model update schemes, which discard outlying measurements or incorporate an estimate of the noise statistics, for example, or adding a gain to Eq. (26) may lessen the predictive algorithm’s sensitivity to noise, but that is beyond the scope of this paper. 4.3.5.Effects of predictive model errorSince the predictive controller relies on an internal model to determine when corrections will be needed, the corrections issued and their timing can be affected by errors in model parameters such as the thermal decay constant . The physical effect of an error in the model’s depends on its sign: for positive errors, the model predicts more rapid temperature changes than actually take place, while for negative errors, the model predicts more gradual changes. This difference can affect the optical performance, depending on the implementation of the predictive controller. For a purely predictive controller that has the correct temperature-to-wavefront model [Eq. (25)] and does not use any measurements to update its internal thermal and wavefront model, the different signs affect the optical performance asymmetrically. For positive errors, the more rapid changes in the predicted temperature correspond directly to more rapid changes in the predicted WFE, so the controller issues corrections more aggressively than strictly necessary. In this case, the controller issues corrections somewhat before is exceeded and overcorrects. For negative errors, the slower changes in the predicted temperature mean that the predicted wavefront changes too slowly, so the RMS WFE may exceed the correction threshold. As a result, the optical performance is less sensitive to positive errors; the penalty for positive errors is a more aggressive correction schedule, while the penalty for negative errors is more time spent over the correction threshold. Therefore, in the situation where the observatory’s true thermal decay constant is not measured precisely, but the relationship between the temperature and the WFE is relatively well known, it may provide better performance to assume a decay constant near the upper end of the uncertainty range. For a predictive controller that uses wavefront measurements to update its internal temperature-to-wavefront model, the effects of positive and negative errors can be more symmetric. In our implementation of the predictive controller, the wavefront measurements are used to adjust the slopes and offsets for the lines relating the predicted temperature to the wavefront coefficients, as described in Sec. 4.2.2. As a result, the controller attempts to compensate for the error by adjusting its linear temperature-to-wavefront model. Typically, these adjustments lead to higher-magnitude slopes and lower-magnitude offsets for negative errors, and the reverse for positive errors. Consequently, for each error type, there are temperatures for which the predictive controller overestimates the wavefront change as well as temperatures for which the predictive controller underestimates the wavefront change, and these temperatures change with each model update. As a result, there is no clear preference for positive or negative errors when the optical performance is averaged over multiple mission schedules, as shown in Fig. 12. It is expected that the predictive controller would similarly attempt to compensate for other model errors, such as incorrect equilibrium temperatures, although these cases have not been investigated in detail yet. Fig. 12Sensitivity to model error. Our implementation of the predictive controller can tolerate significant errors in the modeled thermal decay constant while still providing superior wavefront control. The error mostly affects the amount of time that the RMS WFE exceeds the correction threshold , and the effects are more pronounced at lower since there is less room for the RMS WFE to vary before exceeding . For the hypothetical mission scenarios, the predictive controller successfully maintains the wavefront despite errors as high as 25% (corresponding to a modeled time constant 1 day shorter than the actual time constant) and as low as , spending less than 7% of the time over for as low as 5 nm. 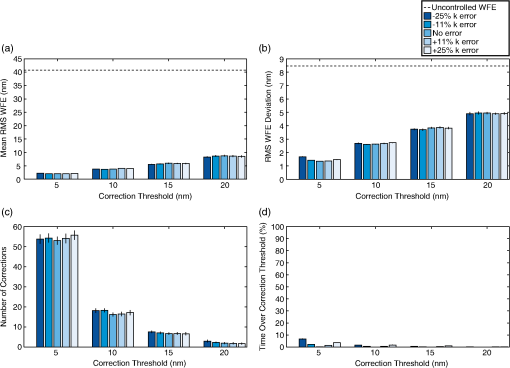 It is clearly advantageous for a predictive controller to have an internal model of the observatory that is as accurate as possible, yet the results in Fig. 12 also show that the predictive controller can tolerate significant discrepancies between the model and the as-built performance while still delivering superior wavefront control. For the sample mission scenarios, the predictive controller successfully functions with errors as high as 25%, which corresponds to a modeled time constant 1 day shorter than the actual time constant, and as low as . The error mostly affects the amount of time that the RMS WFE exceeds the correction threshold, and the effects are more pronounced at lower thresholds since there is less room for the RMS WFE to vary before exceeding . For , the error has little effect on the optical performance: the 25% error, error, and error-free controllers issue approximately the same number of corrections and spend approximately the same amount of time over . If we decrease to 5 nm, the controllers still issue approximately the same number of corrections, but the amount of time over increases with the magnitude of the error. However, even in this case, the predictive controllers all spend less than 7% of the time over , compared to more than 50% for the baseline and averaging algorithms (Fig. 8). 5.ConclusionThe wavefront control problem for an active space telescope at L2 requires a trade between minimizing the WFE and minimizing the number of corrections (actuator moves). Mirror state updates thus happen occasionally rather than continuously, a key difference from typical ground-based active optics systems. Furthermore, since the dominant wavefront perturbations are due to thermal changes caused by variations in the spacecraft attitude with respect to the sun, they are byproducts of the observing schedule, which is known and determined in advance. We have investigated two approaches for improving the effectiveness of wavefront control under these conditions. First, these wavefront perturbations can be controlled passively by introducing scheduling constraints that prevent large temperature swings by limiting the allowable sun angles for each observation in the schedule based on the observation duration and the predicted mean telescope temperature at the start of the observation. Such constraints would need to be weighed against the many other criteria used in scheduling, such as the observatory efficiency and momentum management. Given the need to balance the sun angle restrictions with these other factors, it seems implausible that schedule constraints alone could entirely eliminate the need for periodic active corrections; however, there may be some cases worth pursuing as part of a broader strategy. In particular, since the longest observation blocks most readily lead to large swings in the telescope temperature, attention paid to scheduling those observations could result in more benign schedules without imposing any strict restriction in general. In the case of deep fields or large mosaics, it would be advantageous from a wavefront maintenance perspective to split those observations into multiple noncontiguous blocks provided that doing so is consistent with achieving the science goals of those programs. Alternatively, given any observing schedule, it is possible to predict when the WFE will exceed some correction threshold and to schedule wavefront corrections in advance. In this case, the control problem is naturally expressed as a hybrid control problem since the wavefront evolution is affected by discrete events, such as the start of a new observation or the implementation of a new wavefront correction, as well as continuous dynamics, such as the telescope’s temperature evolution. Using this approach, we have developed a hybrid predictive controller designed to prevent the time-variable component of the RMS WFE from exceeding a desired correction threshold , and compared it to two variants of the baseline control strategy for JWST. During hypothetical mission scenarios, all three algorithms successfully hold the RMS WFE below at least 80% of the time on average, even with wavefront sensor noise levels up to half the correction threshold. The predictive controller generally performs slightly better, holding the RMS WFE below at least 91% of the time on average and approaching 100% for sufficiently low sensing noise. It also has superior performance on our metrics for the mean and temporal deviation of the RMS WFE for most test cases. In addition, the predictive controller can be used with more aggressive than the other algorithms; limited by their fixed correction period, the baseline and averaging algorithms cannot correct aggressively enough to hold the RMS WFE below during times when the wavefront changes rapidly, and the performance flattens out for . The performance of the predictive controller is limited primarily by the allowable number of corrections; the algorithm issues substantially more corrections for lower or higher noise levels. Our implementation of the predictive controller can tolerate significant errors in the modeled thermal decay constant . These errors mostly affect the amount of time that the RMS WFE exceeds the correction threshold, and the effects are more pronounced at lower since there is less room for the RMS WFE to vary before exceeding . For the sample mission scenarios, the predictive controller successfully maintains the wavefront despite errors as high as 25% and as low as , with the RMS WFE exceeding a correction threshold of 5 nm less than 7% of the time on average. Since we used thermal model parameters derived from the requirements for JWST, these quantitative results depend on JWST meeting its design requirements for thermal stability, but more generally they confirm the potential to improve the optical performance of an active space telescope by using more sophisticated control laws. Although the assumed model parameters will differ from the exact numbers in flight, the general behavior and benefits of the predictive controller should hold over a wide range of parameter space for active space telescopes that are perturbed based on predictable external stimuli. The predictive controller is promising in its current form, but additional enhancements are worth considering in future modeling efforts. For example, using temperature measurements to update the temperature model may allow for less frequent wavefront measurements, increasing the observatory efficiency in addition to improving the overall predictions. Combining predictive control with scheduling restrictions for long observations may reduce the number of corrections needed during a mission. Modifications to the predictive controller, such as adding a control gain or incorporating an estimate of the noise statistics in the model update process, may decrease its sensitivity to noise and help to reduce the number of corrections required to maintain the optical performance. Incorporating additional perturbation sources, such as roll around the telescope optical axis, also remains future work, although it is expected that the current algorithms will naturally compensate for slow perturbations such as gradual sunshield degradation or variations in the orbital distance to the sun. The practical details of a hypothetical implementation for JWST are beyond the scope of this paper. However, the presence of the wavefront control software system and its associated trending system on the ground at the Science and Operations center rather than on the spacecraft computer provides more flexibility for future enhancements. Validating thermal and optical models against the as-built performance of the telescope is already planned as part of the ongoing integration and test program. Looking beyond JWST, active optical control is expected to be an essential technology for other future large space telescopes such as the proposed AFTA and ATLAST mission concepts. Active and adaptive control of terrestrial telescopes has matured into a sophisticated field with many specialized algorithms adapted to different conditions. Similarly, we should expect that active telescopes in space will benefit from a variety of control algorithms developed by taking into account the unique circumstances and environment of each mission. AcknowledgmentsWe would like to thank Wayne Kinzel for providing the SODRM schedules; Mark McGinnis and Joe Howard for discussing the thermal models and optical deformations of JWST; and Mark Clampin, Mike Menzel, Roeland van der Marel, and Laurent Pueyo for providing feedback on earlier versions of this work. Parts of the work reported here were supported by NASA Grant NNX07AR82G (PI: Mountain). ReferencesR. N. WilsonF. FranzaL. Noethe,
“Active optics,”
J. Mod. Opt., 34
(4), 485
–509
(1987). http://dx.doi.org/10.1080/09500348714550501 JMOPEW 0950-0340 Google Scholar
The Design and Construction of Large Optical Telescopes, Springer-Verlag, New York
(2003). Google Scholar
R. N. WilsonL. Noethe,
“Closed-loop active optics: its advantages and limitations for correction of wind-buffet deformations of large flexible mirrors,”
Proc. SPIE, 1114 290
–301
(1989). http://dx.doi.org/10.1117/12.960834 PSISDG 0277-786X Google Scholar
R. C. Jaredet al.,
“The W. M. Keck Telescope segmented primary mirror active control system,”
Proc. SPIE, 1236 996
–1008
(1990). http://dx.doi.org/10.1117/12.19266 PSISDG 0277-786X Google Scholar
S. GuisardL. NoetheJ. Spyromilio,
“Performance of active optics at the VLT,”
Proc. SPIE, 4003 154
–164
(2000). http://dx.doi.org/10.1117/12.391506 PSISDG 0277-786X Google Scholar
A. R. Contoset al.,
“Aligning and maintaining the optics for the James Webb Space Telescope (JWST) on-orbit: the wavefront sensing and control concept of operations,”
Proc. SPIE, 6265 62650X
(2006). http://dx.doi.org/10.1117/12.669067 PSISDG 0277-786X Google Scholar
D. S. Actonet al.,
“Wavefront sensing and controls for the James Webb Space Telescope,”
Proc. SPIE, 8442 84422H
(2012). http://dx.doi.org/10.1117/12.925015 PSISDG 0277-786X Google Scholar
J. R. Fienupet al.,
“Hubble Space Telescope characterized by using phase-retrieval algorithms,”
Appl. Opt., 32
(10), 1747
–1767
(1993). http://dx.doi.org/10.1364/AO.32.001747 APOPAI 0003-6935 Google Scholar
J. E. KristC. J. Burrows,
“Phase-retrieval analysis of pre- and post-repair Hubble Space Telescope images,”
Appl. Opt., 34
(22), 4951
–4964
(1995). http://dx.doi.org/10.1364/AO.34.004951 APOPAI 0003-6935 Google Scholar
W. F. Hoffmanet al.,
“Determination of Spitzer Space Telescope focus from IRAC images without a focus slew,”
Proc. SPIE, 5487 186
(2004). http://dx.doi.org/10.1117/12.550649 PSISDG 0277-786X Google Scholar
J. Gersh-Rangeet al.,
“Minimizing the wavefront error degradation for primary mirror segments with failed hexapod actuators,”
Opt. Eng., 51
(1), 011005
(2012). http://dx.doi.org/10.1117/1.OE.51.1.011005 OPEGAR 0091-3286 Google Scholar
D. Spergelet al.,
“Wide-Field Infrared Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA final report,”
(2013). Google Scholar
M. Postmanet al.,
“Advanced Technology Large-Aperture Space Telescope (ATLAST): a technology roadmap for the next decade,”
(2009). Google Scholar
J. S. KnightP. LightseyA. Barto,
“Predicted JWST imaging performance,”
Proc. SPIE, 8442 84422G
(2012). http://dx.doi.org/10.1117/12.926817 PSISDG 0277-786X Google Scholar
D. Di Ninoet al.,
“HST focus variations with temperature,”
(2008). Google Scholar
C. Perrygoet al.,
“Passive thermal control of the NGST,”
Proc. SPIE, 3356 1102
–1113
(1998). http://dx.doi.org/10.1117/12.324510 PSISDG 0277-786X Google Scholar
P. A. Lightseyet al.,
“James Webb Space Telescope: large deployable cryogenic telescope in space,”
Opt. Eng., 51
(1), 011003
(2012). http://dx.doi.org/10.1117/1.OE.51.1.011003 OPEGAR 0091-3286 Google Scholar
M. Werner,
“The Spitzer Space Telescope,”
Opt. Eng., 51
(1), 011008
(2012). http://dx.doi.org/10.1117/1.OE.51.1.011008 OPEGAR 0091-3286 Google Scholar
J. D. Johnstonet al.,
“Integrated modeling activities for the James Webb Space Telescope: structural-thermal-optical analysis,”
Proc. SPIE, 5487 600
–610
(2004). http://dx.doi.org/10.1117/12.551704 PSISDG 0277-786X Google Scholar
W. M. KinzelR. E. Douglas Jr.,
“JWST observation specification and expansion to support planning and scheduling,”
Proc. SPIE, 8448 84480Z
(2012). http://dx.doi.org/10.1117/12.926952 PSISDG 0277-786X Google Scholar
C. Ikpeet al.,
“JWST observatory synchronized thermal study #1 (STS-1) summary,”
Google Scholar
L. Petroet al.,
“Planning to minimize angular momentum,”
(2005). Google Scholar
K. D. Gordonet al.,
“Optimizing the observing efficiency of the James Webb Space Telescope,”
Proc. SPIE, 8448 84481U
(2012). http://dx.doi.org/10.1117/12.926130 PSISDG 0277-786X Google Scholar
R. N. Wilsonet al.,
“Active optics,”
J. Mod. Opt., 38
(2), 219
–243
(1991). http://dx.doi.org/10.1080/09500349114550271 JMOPEW 0950-0340 Google Scholar
J. LlacerR. C. JaredJ. M. Fuertes,
“Analysis of the W. M. Keck telescope primary mirror control loop,”
Proc. SPIE, 1236 1024
–1037
(1990). http://dx.doi.org/10.1117/12.19271 PSISDG 0277-786X Google Scholar
J. Rakoczyet al.,
“Primary mirror figure maintenance of the Hobby-Eberly Telescope using the Segment Alignment Maintenance System,”
Proc. SPIE, 4837 702
–713
(2003). http://dx.doi.org/10.1117/12.456734 PSISDG 0277-786X Google Scholar
P. M. ThompsonD. G. MacMynowskiM. J. Sirota,
“Control analysis of the TMT primary segment assembly,”
Proc. SPIE, 7012 70121N
(2008). http://dx.doi.org/10.1117/12.790287 PSISDG 0277-786X Google Scholar
P. J. Antsaklis,
“A brief introduction to the theory and applications of hybrid systems,”
Proc. IEEE, 88
(7), 879
–887
(2000). http://dx.doi.org/10.1109/JPROC.2000.871299 IEEPAD 0018-9219 Google Scholar
M. D. LemmonK. X. HeI. Markovsky,
“Supervisory hybrid systems,”
IEEE Control Syst., 19
(4), 42
–55
(1999). http://dx.doi.org/10.1109/37.777788 1066-033X Google Scholar
R. AlurD. L. Dill,
“A theory of timed automata,”
Theor. Comput. Sci., 126
(2), 183
–235
(1994). http://dx.doi.org/10.1016/0304-3975(94)90010-8 TCSCDI 0304-3975 Google Scholar
R. Aluret al.,
“Hybrid automata: an algorithmic approach to the specification and verification of hybrid systems,”
Hybrid Systems, 209
–229 Springer-Verlag, Germany
(1993). Google Scholar
F. D. TorrisiA. Bemporad,
“HYSDEL—a tool for generating computational hybrid models for analysis and synthesis problems,”
IEEE Trans. Control Syst. Technol., 12
(2), 235
–249
(2004). http://dx.doi.org/10.1109/TCST.2004.824309 IETTE2 1063-6536 Google Scholar
A. BemporadM. Morari,
“Control of systems integrating logic, dynamics, and constraints,”
Automatica, 35
(3), 407
–427
(1999). http://dx.doi.org/10.1016/S0005-1098(98)00178-2 0005-1098 Google Scholar
D. L. PepyneC. G. Cassandras,
“Optimal control of hybrid systems in manufacturing,”
Proc. IEEE, 88
(7), 1108
–1123
(2000). http://dx.doi.org/10.1109/5.871312 IEEPAD 0018-9219 Google Scholar
C. LivadasJ. LygerosN. A. Lynch,
“High-level modeling and analysis of the Traffic Alert and Collision Avoidance System (TCAS),”
Proc. IEEE, 88
(7), 926
–948
(2000). http://dx.doi.org/10.1109/5.871302 IEEPAD 0018-9219 Google Scholar
R. HorowitzP. Varaiya,
“Control design of an automated highway system,”
Proc. IEEE, 88
(7), 913
–925
(2000). http://dx.doi.org/10.1109/5.871301 IEEPAD 0018-9219 Google Scholar
A. Balluchiet al.,
“Automotive engine control and hybrid systems: challenges and opportunities,”
Proc. IEEE, 88
(7), 888
–912
(2000). http://dx.doi.org/10.1109/5.871300 IEEPAD 0018-9219 Google Scholar
D. Subramanianet al.,
“Control design for a hybrid dynamic system: a NASA life support system,”
Hybrid Systems: Computation and Control, 570
–584 Springer-Verlag, Germany
(2004). Google Scholar
B. Kerkezet al.,
“A hybrid system model of seasonal snowpack water balance,”
in Proc. of the 13th ACM Int. Conf. on Hybrid Systems: Computation and Control,
171
–180
(2010). Google Scholar
J. P. Gardneret al.,
“The James Webb Space Telescope,”
Space Sci. Rev., 123
(4), 485
–606
(2006). http://dx.doi.org/10.1007/s11214-006-8315-7 SPSRA4 0038-6308 Google Scholar
P. J. CampoM. Morari,
“Robust model predictive control,”
in Proc. of the 1987 American Control Conf.,
1021
–1026
(1987). Google Scholar
P. A. LightseyA. A. BartoJ. Contreras,
“Optical performance for the James Webb Space Telescope,”
Proc. SPIE, 5487 825
–832
(2004). http://dx.doi.org/10.1117/12.550091 PSISDG 0277-786X Google Scholar
BiographyJessica Gersh-Range recently completed a PhD degree in mechanical engineering at Cornell University. She was the recipient of a NASA Graduate Student Researchers Program fellowship at Marshall Space Flight Center, and she has also worked at the Space Telescope Science Institute as a graduate student. She received a BA degree in physics from Swarthmore College in 2006, with a minor in mathematics. Her research interests include space optical systems, which combines her physics and engineering backgrounds. Marshall D. Perrin is an associate astronomer at the Space Telescope Science Institute, and a member of the telescopes team there. His research interests focus on the development of advanced instrumentation and data processing methods for the characterization of extrasolar planetary systems, including adaptive optics, coronagraphy, integral field spectroscopy, and differential polarimetry. He received his PhD degree from the University of California, Berkeley, and was a postdoc in the UCLA Infrared Lab before joining STScI. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

